Exceptional isomorphism

In mathematics, an exceptional isomorphism, also called an accidental isomorphism, is an isomorphism between members a_i and b_j of two families (usually infinite) of mathematical objects, that is not an example of a pattern of such isomorphisms.^{[note 1]} These coincidences are at times considered a matter of trivia,^[1] but in other respects they can give rise to other phenomena, notably exceptional objects.^[1] In the below, coincidences are listed in all places they occur.

1 Groups
2 Lie theory
3 See also
4 References
5 References

Groups

Finite simple groups

The exceptional isomorphisms between the series of finite simple groups mostly involve projective special linear groups and alternating groups, and are:^[1]

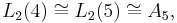$L_2(4) \cong L_2(5) \cong A_5,$ the smallest non-abelian simple group (order 60);

$L_2(7) \cong L_3(2),$ the second-smallest non-abelian simple group (order 168) – PSL(2,7);

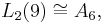
$L_2(9) \cong A_6,$

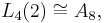
$L_4(2) \cong A_8,$

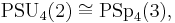$\operatorname{PSU}_4(2) \cong \operatorname{PSp}_4(3),$ between a projective special orthogonal group and a projective symplectic group.

Groups of Lie type

In addition to the aforementioned, there are some isomorphisms involving SL, PSL, GL, PGL, and the natural maps between these. For example, the groups over 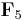$\mathbf{F}_5$ have a number of exceptional isomorphisms:

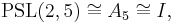$\operatorname{PSL}(2,5) \cong A_5 \cong I,$ the alternating group on five elements, or equivalently the icosahedral group;

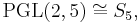$\operatorname{PGL}(2,5) \cong S_5,$ the symmetric group on five elements;

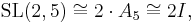$\operatorname{SL}(2,5) \cong 2\cdot A_5 \cong 2I,$ the double cover of the alternating group A₅, or equivalently the binary icosahedral group.

Alternating groups and symmetric groups

There are coincidences between alternating groups and small groups of Lie type:

$L_2(4) \cong L_2(5) \cong A_5,$

$L_2(9) \cong A_6,$

$L_4(2) \cong A_8,$

$O_6(2) \cong S_8.$

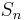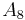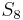These can all be explained in a systematic way by using linear algebra (and the action of $S_n$ on affine $n$ -space) to define the isomorphism going from the right side to the left side. (The above isomorphisms for $A_8$ and $S_8$ are linked via the exceptional isomorphism 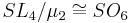$SL_4/\mu_2 \cong SO_6$ .) There are also some coincidences with symmetries of regular polyhedra: the alternating group A5 agrees with the icosahedral group (itself an exceptional object), and the double cover of the alternating group A5 is the binary icosahedral group.

Trivial group

The trivial group arises in numerous ways; families often start with the trivial group which is discarded. For instance, it is:

C1, the cyclic group of order 1;
A0 = A1 = A2, the alternating group on 0, 1, or 2 letters;
S0 = S1, the symmetric group on 0 or 1 letters;
GL(0,K) = SL(0,K) = PGL(0,K) = PSL(0,K), groups of a 0-dimensional vector space;
SL(1,K) = PGL(1,K) = PSL(1,K), groups of a 1-dimensional vector space;
and many others.

Cyclic groups

Cyclic groups of small order especially arise in various ways, for instance:

C2 = ±1 = S⁰ (real numbers of unit norm) = O(1) = Spin(1) = Z^* (group of units of the integers)

Spheres

The spheres S⁰, S¹, and S³ admit group structures, which arise in various ways:

S⁰=O(1)=Spin(1) (this last properly a double cover);
S¹=SO(2)=U(1)=Spin(2) (this last properly a double cover; arising from Real/Complex structures);
S³=Spin(3)=SU(2)=Sp(1) (arising from Real/Complex/Quaternionic structures, respectively)

Coxeter groups

There are some exceptional isomorphisms of Coxeter diagrams, yielding isomorphisms of the corresponding Coxeter groups and of polytopes realizing the symmetries. These are:

A2 = I2(2) (2-simplex is regular 3-gon/triangle);
BC2 = I2(4) (2-cube (square) = 2-cross-polytope (diamond) = regular 4-gon)
A3 = D3 (3-simplex (tetrahedron) is 3-demihypercube (demicube), as per diagram)
A1 = B1 = C1 (= D1?)
D2 = A1 × A1
A4 = E4
D5 = E5

Closely related ones occur in Lie theory for Dynkin diagrams.

Lie theory

In low dimensions, there are isomorphisms among the classical Lie algebras and classical Lie groups called accidental isomorphisms. For instance, there are isomorphisms between low dimensional spin groups and certain classical Lie groups, due to low dimensional isomorphisms between the root systems of the different families of simple Lie algebras, visible as isomorphisms of the corresponding Dynkin diagrams:

Trivially, A0 = B0 = C0 = D0
A1 = B1 = C1 (= D1?)
B2 = C2
D2 = A1 × A1; note that these are disconnected, but part of the D-series
A3 = D3
A4 = E4; the E-series usually starts at 6, but can be started at 4, yielding isomorphisms
D5 = E5

Spin(1) = O(1)

Spin(2) = U(1) = SO(2)

Spin(3) = Sp(1) = SU(2)

Spin(4) = Sp(1) × Sp(1)

Spin(5) = Sp(2)

Spin(6) = SU(4)

References

^ Because these series of objects are presented differently, they are not identical objects (do not have identical descriptions), but turn out to describe the same object, hence one refers to this as an isomorphism, not an equality (identity).

References

^ ^a ^b ^c Wilson, Robert A. (2009), "Chapter 1: Introduction", The finite simple groups, Graduate Texts in Mathematics 251, 251, Berlin, New York: Springer-Verlag, doi:10.1007/978-1-84800-988-2, ISBN 978-1-84800-987-5, Zbl 05622792, http://www.maths.qmul.ac.uk/~raw/fsgs_files/intro.ps, 2007 preprint; Chapter doi:10.1007/978-1-84800-988-2_1.

Exceptional isomorphism

Contents

Groups

Finite simple groups

Groups of Lie type

Alternating groups and symmetric groups

Trivial group

Cyclic groups

Spheres

Coxeter groups

Lie theory

See also

References

References